Process Simulation
Nima Ramezani
30/03/2022
process_simulation.RmdIntroduction
In the previous session, we learned how to run a random-walk simulation to estimate probability distribution over various statuses of the transition system.
As you can see, Random-walk simulation does not give any estimation of the future status of an individual case, but returns the overall status probabilities for all cases.
In this article, we want to predict the future transitions of cases using process simulation. Assume that we are in a certain point in the time-line within the process. Let’s call it the cutpoint time. Some cases have not started yet, some cases are in the middle of their lifetime and some have ended while live cases can be at various statuses within the transitiopn system. Now, let’s stop at the cutpoint time and try to predict(estimate) the next transitions for each case. The Transition Matrix gives us a probability distribution for the next transition of each case. The simulation engine starts with generating a destination for each case as well as a transition time based on the current status of each case. This will generate a list of status transition events for all live cases. After this step, each case will be in a different status and hence different probabiliy distributions and avergae transition times for the next transition. Similarly, another transition is generated for each case and this iterative procedure continues until all the existing cases reach the END status.
For those cases started after the cutpoint time, the simulation engine can generate the case arrival events or use the actual case arrivals by keeping START transitions for the simulation engine to generate next transitions. The former option is a pure prediction as it assumes we have no information of the future arrivals.
We used dataset hospital_billing from package eventdata for this study and choose column activity as the case status:
hospital_df = eventdataR::hospital_billing %>% as.data.frame
tsobj = new('TransitionSystem')Pre-processing
Before feeding the history of transition events to the object, we need to specify which cases start or end within the timeline window of analysis. Most datasets contain a subset of transition events within a window in the time-line. They do not have events outside this window. For example, looking at the range of event times, shows the Timeline Window of Observation (TWO) is from 2012-12-13 10:13:18 to 2015-12-13 13:55:15. We want to specify which cases start or end within the TWO.
We build a simple case profile table to see the first and last activity of each case and number of transitions:
case_profile = hospital_df %>%
arrange(case_id, timestamp) %>%
group_by(case_id) %>%
summarise(first_activity = first(activity),
last_activity = last(activity),
num_transitions = length(activity) - 1) %>%
ungroup
knitr::kable(case_profile %>% head(10))| case_id | first_activity | last_activity | num_transitions |
|---|---|---|---|
| A | NEW | BILLED | 4 |
| AA | NEW | BILLED | 5 |
| AAA | NEW | NEW | 0 |
| AAB | NEW | NEW | 0 |
| AAC | NEW | BILLED | 5 |
| AAD | NEW | NEW | 0 |
| AAE | NEW | BILLED | 11 |
| AAF | NEW | DELETE | 1 |
| AAG | NEW | BILLED | 7 |
| AAH | NEW | BILLED | 4 |
We can see that some cases have only one status(activity) or zero transitions. The single activity of those cases is:
NEW. To remove outliers in the overall end-to-end case process times (durations), we specify these cases as incomplete by specifying that process end falls outside the TWO. We do this by adding a flag column to the input table which specifies which cases end within the TWO. This is a simple pre-processing that needs to be done before feeding the data to the object:
Build and observe the object
Now, feed the input dataset to the object:
tsobj$feed.transition_events(hospital_df,
caseID_col = 'case_id',
status_col = 'activity',
startTime_col = 'timestamp',
caseEndFlag_col = 'case_ended')## Warning:
##
## 1 events removed due to missing values in column caseID
## Let’s now filter out single-status cases as well as 1% of the cases with the most uncommon traces to get a more readable process map:
tsobj$set.filter.case(complete = T, freq_rate_cut = 0.99)##
## Aggregating links ...Done!
tsobj$plot.process.map(config = list(direction = 'left.right'), width = "800px")##
## Aggregating nodes ...Done!
##
## Aggregating links ...Done!Run Simulation
The time range of the process is from 2012-12-13 10:13:17 until 2015-12-13 13:55:16. We choose some time in the middle like 2013-07-01 and generate transitions from that time for the next two years.
Method run.simulation runs a simulation from the start date-time that you specify and returns generated transitions in a new event-log:
new_transitions_gaussian = tsobj$run.simulation(start_dt = '2013-03-01', target_dt = '2014-03-01', training_time_range = 'simulation')##
## Aggregating links ...Done!
##
## Aggregating links ...Done!| caseID | status | nextStatus | startTime | meanTime | sdTime | pred_duration | nxtTrTime |
|---|---|---|---|---|---|---|---|
| A | NEW | CHANGE DIAGN | 2012-12-16 19:33:10 | 3.897164e+05 | 1.352020e+06 | 6676456.66 | 2013-03-04 02:07:26 |
| A | CHANGE DIAGN | FIN | 2013-03-04 02:07:26 | 6.250932e+06 | 2.831556e+06 | 2684091.16 | 2013-04-04 03:42:17 |
| A | FIN | RELEASE | 2013-04-04 03:42:17 | 1.164899e+05 | 1.022184e+06 | 28800.64 | 2013-04-04 11:42:18 |
| A | RELEASE | CODE OK | 2013-04-04 11:42:18 | 3.866698e+05 | 5.895277e+05 | 457323.89 | 2013-04-09 18:44:22 |
| A | CODE OK | BILLED | 2013-04-09 18:44:22 | 4.846466e+06 | 4.037759e+06 | 10903371.24 | 2013-08-13 23:27:13 |
| A | BILLED | END | 2013-08-13 23:27:13 | 1.000000e+00 | 0.000000e+00 | 1.00 | 2013-08-13 23:27:14 |
| AA | CODE OK | BILLED | 2013-02-18 01:44:10 | 4.846466e+06 | 4.037759e+06 | 11856281.15 | 2013-07-05 07:08:51 |
| AA | BILLED | STORNO | 2013-07-05 07:08:51 | 1.235464e+06 | 2.006639e+06 | 279410.78 | 2013-07-08 12:45:41 |
| AA | STORNO | BILLED | 2013-07-08 12:45:41 | 2.885252e+05 | 1.375072e+06 | 2252611.05 | 2013-08-03 14:29:12 |
| AA | BILLED | STORNO | 2013-08-03 14:29:12 | 1.235464e+06 | 2.006639e+06 | 3853610.62 | 2013-09-17 04:56:03 |
| AA | STORNO | REJECT | 2013-09-17 04:56:03 | 1.024339e+06 | 2.892600e+06 | 3769726.14 | 2013-10-30 20:04:49 |
| AA | REJECT | BILLED | 2013-10-30 20:04:49 | 5.149046e+05 | 1.021344e+06 | 2391295.01 | 2013-11-27 12:19:44 |
| AA | BILLED | END | 2013-11-27 12:19:44 | 1.000000e+00 | 0.000000e+00 | 1.00 | 2013-11-27 12:19:45 |
| AAC | CODE OK | BILLED | 2013-01-22 01:37:36 | 4.846466e+06 | 4.037759e+06 | 3767134.75 | 2013-03-06 16:03:10 |
| AAC | BILLED | END | 2013-03-06 16:03:10 | 1.000000e+00 | 0.000000e+00 | 1.00 | 2013-03-06 16:03:11 |
| AAF | NEW | NEW | 2013-01-31 21:17:48 | 1.018364e+00 | 4.105588e-01 | 2428932.00 | 2013-03-01 00:00:00 |
| AAF | NEW | CHANGE DIAGN | 2013-03-01 00:00:00 | 3.897164e+05 | 1.352020e+06 | 608420.37 | 2013-03-08 01:00:20 |
| AAF | CHANGE DIAGN | FIN | 2013-03-08 01:00:20 | 6.250932e+06 | 2.831556e+06 | 8089995.41 | 2013-06-09 16:13:35 |
| AAF | FIN | RELEASE | 2013-06-09 16:13:35 | 1.164899e+05 | 1.022184e+06 | 494049.59 | 2013-06-15 09:27:45 |
| AAF | RELEASE | CODE OK | 2013-06-15 09:27:45 | 3.866698e+05 | 5.895277e+05 | 118441.73 | 2013-06-16 18:21:47 |
What you get is a list of predicted auto-generated transition events that happen after the simulation start date 2014-07-01. These events represent one of the many ways that the process could have continued after the specified start date. The simulation engine generates two values for each transition:
Transition Target: is determined based on the probability distribution for transition to the next targets given the current status of a case.
Transition Time: time or duration the cases linger at the source status before migrating to the next status. Transition time is by default generated as a random value with normal distribution with mean and standard deviation observed from the history of transitions of each type.
But are transition times really follow a normal distribution? Let’s look at the distributions of the transition times in the transition system. Function plot_transition_time_histogram can give you this visualization (you will need to install packages plotly and crosstalk):
if(!require(plotly)){install.packages('plotly')}
if(!require(crosstalk)){install.packages('crosstalk')}
tsobj %>% plot_transition_time_histogram(remove_outliers = TRUE)Select a transition from the drop-down menu to see a histogram of the durations. You can choose transitions with higher frequencies like FIN-RELEASE, RELEASE-CODE OK or CODE OK-BILLED. How many of them look like having a gaussian distribution? You can see that most durations have a distribution similar to exponential. That’s why selecting normal distribution in generating transition times may lead to unrealistic results.
You can generate transition times based on exponential distribution by passing exp to argument family:
new_transitions_exp = tsobj$run.simulation(start_dt = '2013-03-01', target_dt = '2014-03-01', family = 'exp')##
## Aggregating links ...Done!
##
## Aggregating links ...Done!| caseID | status | nextStatus | startTime | meanTime | sdTime | pred_duration | nxtTrTime |
|---|---|---|---|---|---|---|---|
| A | NEW | DELETE | 2012-12-16 19:33:10 | 616102.32 | 877460.5 | 1.007734e+07 | 2013-04-12 10:48:53 |
| A | DELETE | END | 2013-04-12 10:48:53 | 1.00 | 0.0 | 3.522212e+00 | 2013-04-12 10:48:57 |
| AA | CODE OK | BILLED | 2013-02-18 01:44:10 | 919210.95 | 639235.6 | 3.786179e+06 | 2013-04-02 21:27:09 |
| AA | BILLED | END | 2013-04-02 21:27:09 | 1.00 | 0.0 | 1.209429e+00 | 2013-04-02 21:27:10 |
| AAC | CODE OK | BILLED | 2013-01-22 01:37:36 | 919210.95 | 639235.6 | 3.309722e+06 | 2013-03-01 08:59:38 |
| AAC | BILLED | END | 2013-03-01 08:59:38 | 1.00 | 0.0 | 1.093464e-01 | 2013-03-01 08:59:38 |
| AAF | NEW | CHANGE DIAGN | 2013-01-31 21:17:48 | 32187.09 | 153605.5 | 2.428932e+06 | 2013-03-01 00:00:00 |
| AAF | CHANGE DIAGN | DELETE | 2013-03-01 00:00:00 | 481658.17 | 951958.9 | 2.243776e+05 | 2013-03-03 14:19:37 |
| AAF | DELETE | END | 2013-03-03 14:19:37 | 1.00 | 0.0 | 7.561899e-01 | 2013-03-03 14:19:38 |
| AAH | NEW | CHANGE DIAGN | 2013-02-08 15:11:34 | 32187.09 | 153605.5 | 1.759706e+06 | 2013-03-01 00:00:00 |
| AAH | CHANGE DIAGN | FIN | 2013-03-01 00:00:00 | 782110.38 | 1035421.6 | 2.704017e+05 | 2013-03-04 03:06:41 |
| AAH | FIN | RELEASE | 2013-03-04 03:06:41 | 103164.70 | 224167.7 | 2.904877e+04 | 2013-03-04 11:10:50 |
| AAH | RELEASE | CODE OK | 2013-03-04 11:10:50 | 90384.63 | 168560.0 | 1.391668e+05 | 2013-03-06 01:50:17 |
| AAH | CODE OK | BILLED | 2013-03-06 01:50:17 | 919210.95 | 639235.6 | 3.569060e+05 | 2013-03-10 04:58:43 |
| AAH | BILLED | END | 2013-03-10 04:58:43 | 1.00 | 0.0 | 7.757981e-01 | 2013-03-10 04:58:44 |
| AAI | START | NEW | 2013-03-12 09:05:06 | 1.00 | 0.0 | 1.374038e+00 | 2013-03-12 09:05:07 |
| AAI | NEW | FIN | 2013-03-12 09:05:07 | 237290.93 | 719721.9 | 1.886645e+04 | 2013-03-12 14:19:33 |
| AAI | FIN | RELEASE | 2013-03-12 14:19:33 | 103164.70 | 224167.7 | 3.820031e+04 | 2013-03-13 00:56:14 |
| AAI | RELEASE | CODE OK | 2013-03-13 00:56:14 | 90384.63 | 168560.0 | 2.154728e+04 | 2013-03-13 06:55:21 |
| AAI | CODE OK | BILLED | 2013-03-13 06:55:21 | 919210.95 | 639235.6 | 2.026849e+05 | 2013-03-15 15:13:26 |
Compare the distribution of transition durations of the two generated eventlogs:
new_transitions_gaussian %>% filter(status == "FIN", nextStatus == "RELEASE") %>% pull(pred_duration) %>%
hist(breaks = 1000, main = "Histogram of Generated durations for FIN-RELEASE \n (family = 'normal')",
xlab = "transition time (sec)")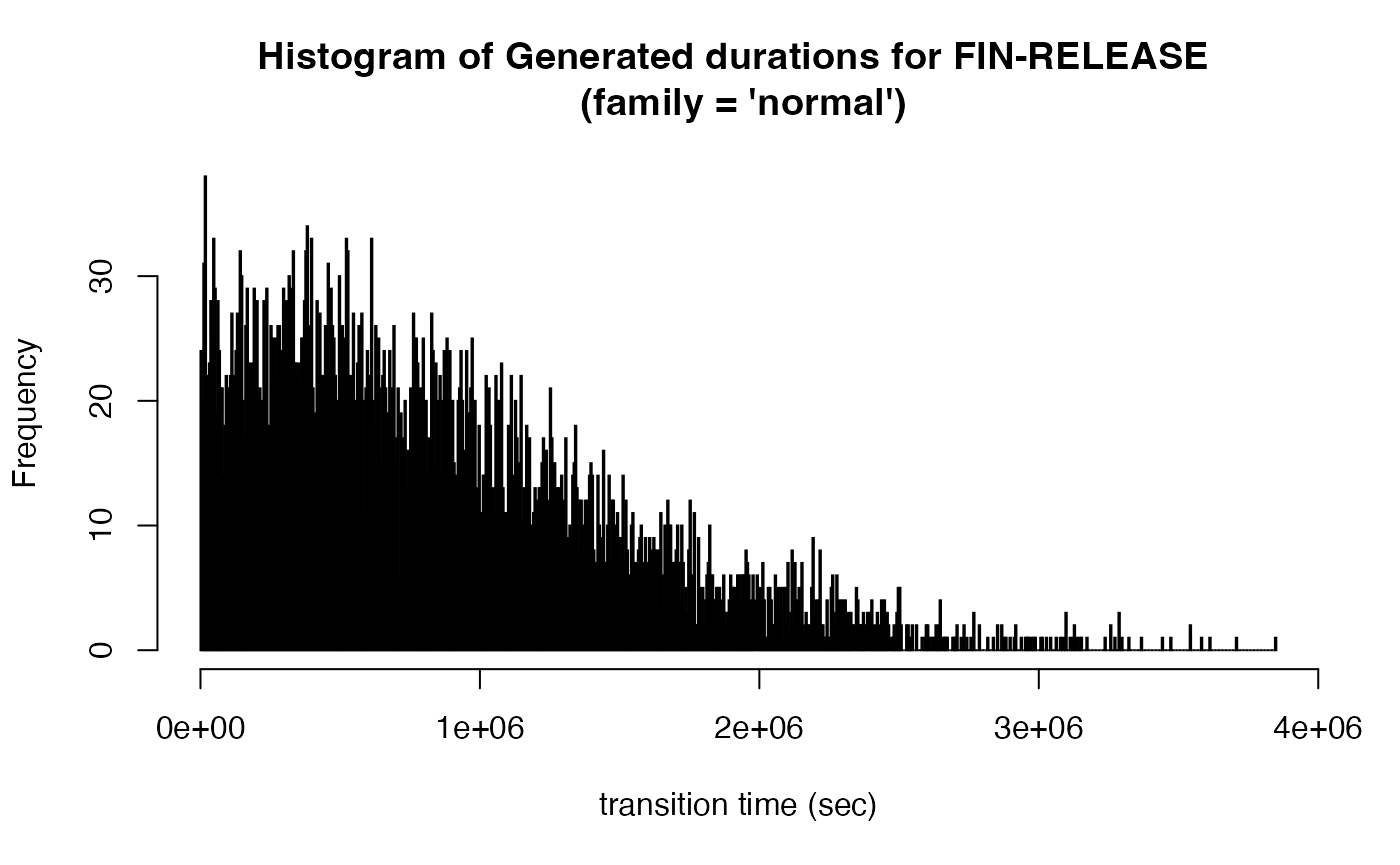
new_transitions_exp %>% filter(status == "FIN", nextStatus == "RELEASE") %>% pull(pred_duration) %>%
hist(breaks = 1000, main = "Histogram of Generated durations for FIN-RELEASE \n (family = 'exp')",
xlab = "transition time (sec)")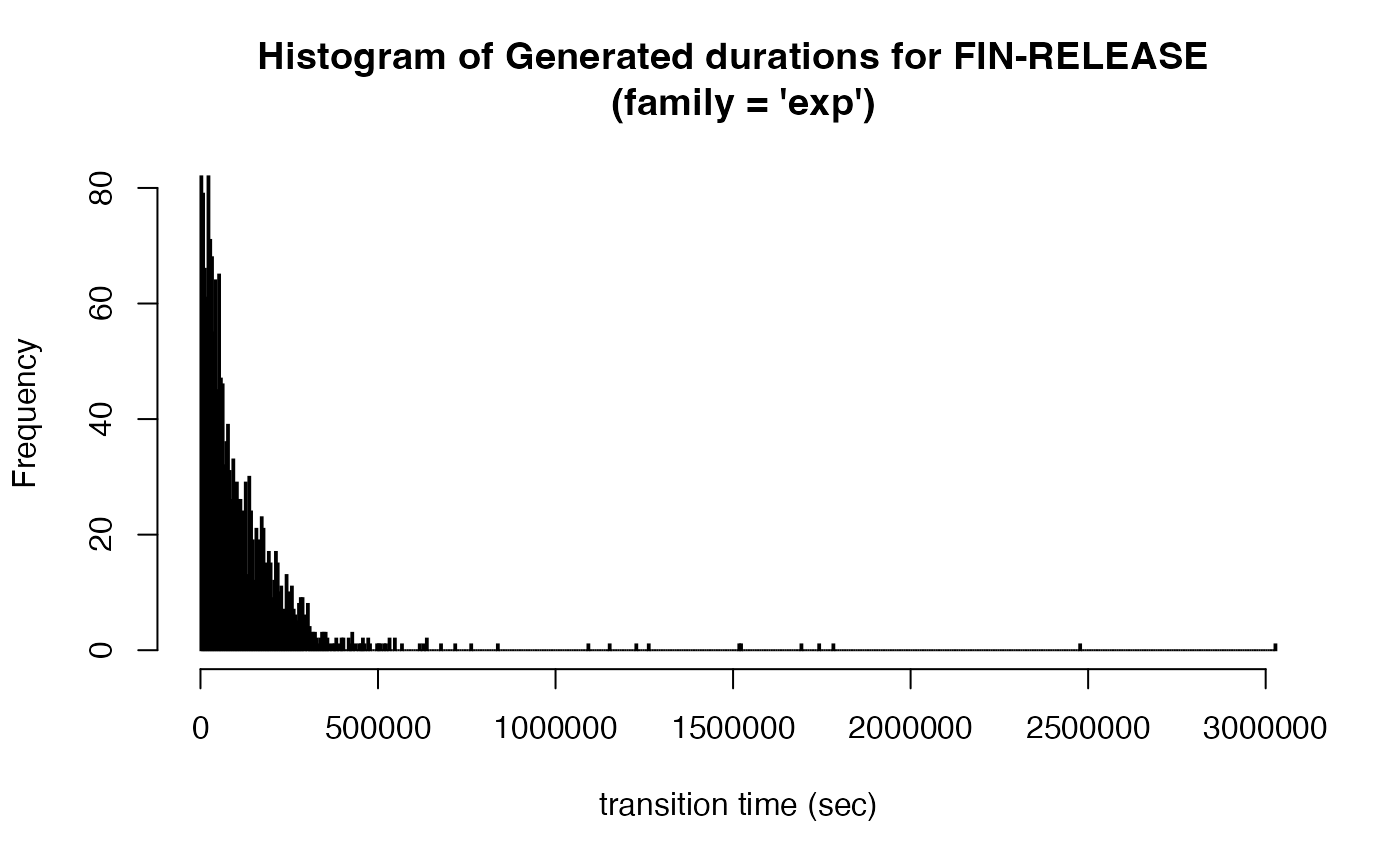
You can change the time generator engine of the simulator and set it to your custom function. By default the simulator uses function markovchain_transition_time_estimator to generate predicted transition durations. This function is called multiple times during the simulation. The simulator engine passes three inputs to this function:
histobj: an object of classTransitionSystem.histobjwill directly be passed to this function. During the simulation, the simulator engine changes the current time fromstart_dtto thetarget_dt. Thehistobjobject, contains process history data upto the current time.input: dataframe containig the list of transition events up to the current time.curent_time: the value of the current time
The output of this function must be a dataframe with added column pred_duration containing the estimated or predicted durations.
Simulation on a Periodic Transition System
Predicting transition durations is tricky and complicated, because you will need to respect the distribution of the observed durations in the regressor model or any time generator engine you are using.
Similarly to what we have seen in the Random Walk Analysis, using Periodic Transition Systems is a way to avoid complexities of time prediction.
Let’s build a Periodic Transition System from the object we have and run a simulation:
ts_monthly = tsobj$to_periodic('month')##
## Verifications started ... Done!
##
## Managing event times ... Done!
##
## Creating time ends and event attribute maps ... Done!
##
## Adding clock events ... Done!
##
## Creating variable last value table ... Done!
new_transitions_periodic = ts_monthly$run.simulation(start_dt = '2013-03-01', target_dt = '2014-03-01', training_time_range = 'simulation')##
## Aggregating links ...Done!The generated table shows the predicted status of each case on each day. This prediction is of course not expected to be very accurate in the individual level because we have not used any case-specific features, however, it provides a good overall estimation of expected process key metrics like turnaround (end-to-end) time, meeting Service Level Agreements (SLA) on all or a specific subset of cases and daily volume of arrivals to each status (activity in this example).
Comparing some metrics
Here, we will compare some of the actual and predicted metrics like average end-to-end process time by building a Tranition System object from the event-logs generated by simulation.
# Actual subset of transitions for the duration of simulation:
actual = tsobj$extract_subset(time_from = '2013-03-01', time_to = '2014-03-01')
actual$set.filter.case(complete = T)
# simulated object associated with the gaussian generated transitions
simulated_gaussian = new("TransitionSystem")
index_started_before = which(new_transitions_gaussian$startTime < '2013-03-01')
new_transitions_gaussian %>% group_by(caseID) %>%
summarise(first_status = first(status), last_status = last(nextStatus),
min_time = min(startTime), max_time = max(startTime)) %>% ungroup -> case_profile
new_transitions_gaussian %>% left_join(case_profile, by = "caseID") %>%
mutate(case_started = (first_status == "START"), case_ended = last_status == "END") %>%
simulated_gaussian$feed.transition_events(caseStartFlag_col = 'case_started', caseEndFlag_col = 'case_ended')
simulated_gaussian$set.filter.case(complete = T)
# simulated object associated with the exponential generated transitions
simulated_exp = new("TransitionSystem")
index_started_before = which(new_transitions_exp$startTime < '2013-03-01')
new_transitions_exp %>% group_by(caseID) %>%
summarise(first_status = first(status), last_status = last(nextStatus),
min_time = min(startTime), max_time = max(startTime)) %>% ungroup -> case_profile
new_transitions_exp %>% left_join(case_profile, by = "caseID") %>%
mutate(case_started = (first_status == "START"), case_ended = last_status == "END") %>%
simulated_exp$feed.transition_events(caseStartFlag_col = 'case_started', caseEndFlag_col = 'case_ended')
simulated_exp$set.filter.case(complete = T)
# simulated object associated with the periodic generated transitions
simulated_periodic = new('TransitionSystem')
# Cases that ended within the simulation time range"
ended_cases = new_transitions_periodic[new_transitions_periodic$nextStatus == "END", "caseID", drop = T] %>% unique
new_transitions_periodic$case_ended = new_transitions_periodic$caseID %in% ended_cases
simulated_periodic$feed.transition_events(new_transitions_periodic, remove_sst = T, caseStartTags = "START", caseEndFlag_col = "case_ended")
simulated_periodic$set.filter.case(complete = T)
att_actual = "Average Turnaround Time (Actual): %s" %>%
sprintf(actual$get.metric('avgTT', time_unit = 'day'))
att_gaussian = "Average Turnaround Time (Simulated Gaussian): %s" %>%
sprintf(simulated_gaussian$get.metric('avgTT', time_unit = 'day'))
att_exp = "Average Turnaround Time (Simulated Exponential): %s" %>%
sprintf(simulated_exp$get.metric('avgTT', time_unit = 'day'))
att_periodic = "Average Turnaround Time (Simulated Periodic): %s" %>%
sprintf(simulated_periodic$get.metric('avgTT', time_unit = 'day'))
ant_actual = "Average Number of Transitions (Actual): %s" %>%
sprintf(actual$get.metric('avgTrans'))
ant_gaussian = "Average Number of Transitions (Simulated Gaussian): %s" %>%
sprintf(simulated_gaussian$get.metric('avgTrans'))
ant_exp = "Average Number of Transitions (Simulated Exponential): %s" %>%
sprintf(simulated_exp$get.metric('avgTrans'))
ant_periodic = "Average Number of Transitions (Simulated Periodic): %s" %>%
sprintf(simulated_periodic$get.metric('avgTrans'))
cat(att_actual, "\n", att_gaussian, "\n", att_exp, "\n", att_periodic, "\n", "\n",
ant_actual, "\n", ant_gaussian, "\n", ant_exp, "\n", ant_periodic, "\n")## Average Turnaround Time (Actual): 140.12
## Average Turnaround Time (Simulated Gaussian): 172.7
## Average Turnaround Time (Simulated Exponential): 10.13
## Average Turnaround Time (Simulated Periodic): 145.96
##
## Average Number of Transitions (Actual): 5.12
## Average Number of Transitions (Simulated Gaussian): 5
## Average Number of Transitions (Simulated Exponential): 2.09
## Average Number of Transitions (Simulated Periodic): 1.9